After learning more and more about functional programming, a lot of the operations that we usually do in Java, or JavaScript, and other imperative languages, are implemented recursively.

There are some pros and cons about writing code around immutability - you think more functionally.

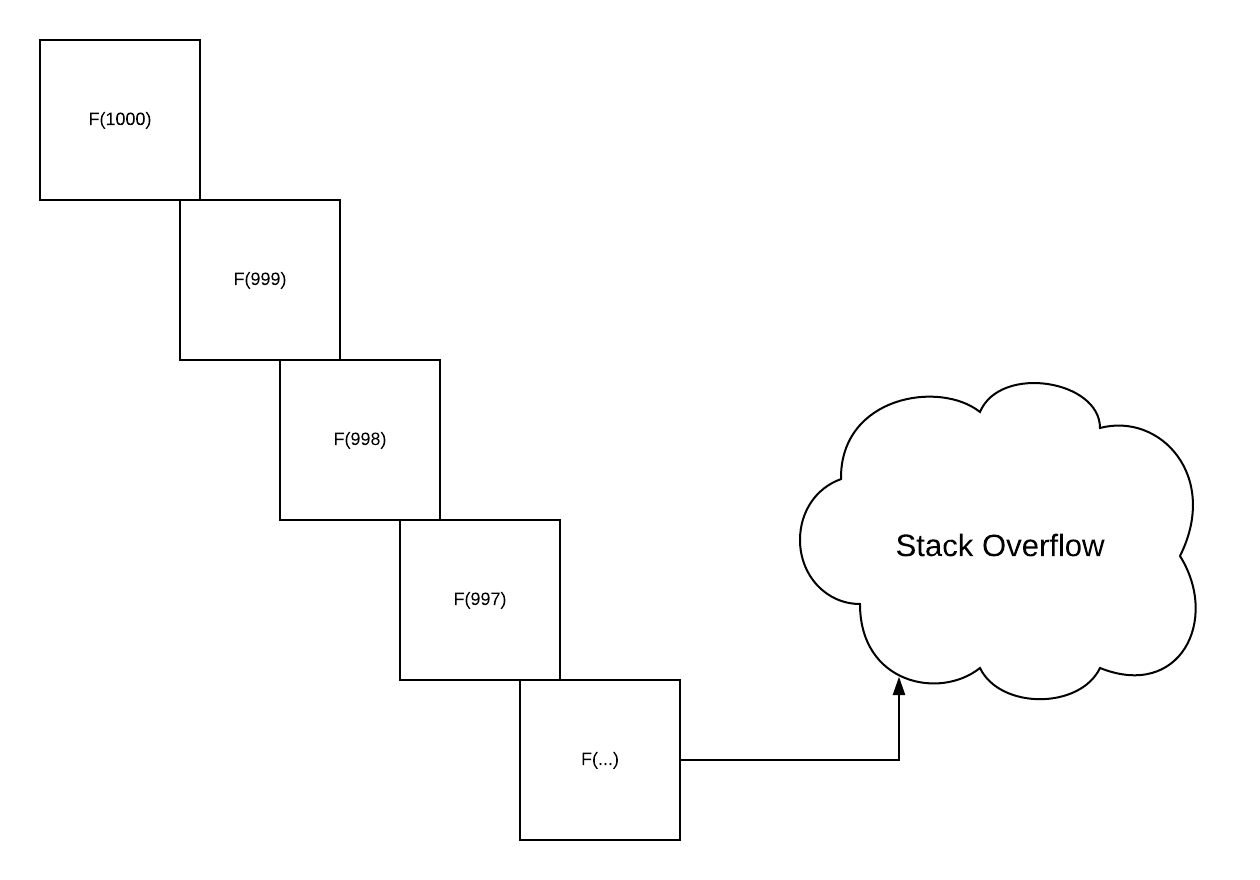
In Scala, recursion is usually implemented with stack underneath. For most of the operations that you do, recursion works fine. However, if you want to process a massive amount of data in sync - that needs to loop through the data to transform to another always - it can blow up your stack and said stack overflow.

How would you defer this situation for programming a vast data set functionally?

My friend, the answer is using Eval. It is a cats data type for controlling synchronous data evaluation.

Before we get into that, let me tell you a little bit about the three mechanisms of the Scala modifier and how it is essential to leverage them to optimize the performance of your application.

What is Eager?

Eager computations happen when you declare the computation, it evokes it right away. For instance, val in Scala evokes the value inside that computation right way when you declare it.

What is Lazy?

Lazy computation is the opposite of Eager. It evokes the computation when you evoke them. For instance, if you define def in Scala, that computation is not evoked right away. The function gets called when you evoke the function the second time.

What is Memoized?

Memoize computation is like a cache that stores the result of your initial call on that computation so that next time when you call that computation, it retrieves it from the cache.

For instance, when once you declare a val in Scala, and when you retrieve the computation again, it will memoize it.

val x = {
  println(s"hi, I am eager and memoized!")
  math.random
}
// hi, I am eage and memoized!
// x: Double = 0.09227668662578081


// first access 
x
// res0: Double = 0.09227668662578081

// second access
x
// res1: Double = 0.09227668662578081

Eval as a Monad

Cats Eval has 3 types: now, always, later, that behaves the same as the scala models of evaluation.

The way you import and the define the constructor parameter like this, it creates a instance of eval type:

import cats.Eval
val now = Eval.now(math.random + 1000) // this will evaluate right away
val always = Eval.always(math.random + 2000)
val later = Eval.later(math.random + 3000)

You can extract the result of the Eval instance that you created by evoking the value method.

now.value

Eval.now is equivalent to val - it is eager and memoized. Eval.always is equivalent to def - it is lazy, and not memoized. Eval.later is equivalent to lazy - it is lazy, and it is memoized.

Knowing this, you can construct map and flatMap through Eval because it is a Monad.

val greetings = for {
  hi <- Eval.now {
      println("hi is evoke.")
      s"hi with random math : $math.random"
    }
  world <- Eval.always {
      println("always is evoke.")
      "world -- $math.random"
  }
} yield hi + world

// first access, which one gets evoke? What will the value?
greetings.value

// second access, which one gets evoke what will the value?
greetings.value

The code above, Eval.now first gets printed, and calculate. However, the first access, and other access, the world is evaluated and goes to the yield section to evaluate the hi+world.

Which one,hi or world, will the math.random be evaluated each access?

Eval has a memoize functionality that able to memoized all the computation leading up. Let me give you an example:

val x = Eval.always{println("First step")}
          .map(_ => println("Second Step"))
          .memoize
          .map(_ =>  println("Third Step"))
          
// first access
x.value
// First Step
// Second Step
// Third Step

// second access 
x.value
// Third Step

Note to takeaway: If you have a computation sequence, which there is only 1 step that is continuously changing, you can do memoize in the computation to increase its performance.

Usually, when we compute recursive calls in a large number of numbers, we encounter stack-overflow. Eval.defer can help you defer your computation from the stack and store them in the heap so that you can compute a large amount of computation recursively.

Simple example of a factorial:

def factorial(x:BigInt) : BigInt = if(x == 0) {
  1
} else {
  factorial(x-1) * x
}

factorial(500000) // this will blow up your stack

With a little twist of Eval you can compute your BigInt factorial

def factorialEval(x: BigInt): Eval[BigInt] = if(x == 0) {
  Eval.now(1)
} else {
  Eval.defer(factorialEval(x-1).map(_ * x))
}

// incorporate in your original factorial method
def factorial(x:BigInt):BigInt = factorialEval(x).value

One practice item:

Can you transformed foldRight to Eval?

def foldRight[A,B](as:List[A], acc:B)(fn:(A,B) => B):B = as match {
  case head::tail =>
    fn(head, foldRight(tail,acc)(fn))
  case Nil =>
    acc
}

Main Takeaway:

• There are 3 terms of computation - eager, lazy, memoized
• Eval has the same 3 terms as Scala - Eval.now, Eval.always, Eval.later
• You can memoize your computation sequence and also create a (not entirely) stack free computation using Eval to optimized your computation on extensive data and data structure.

Like this Article?

Sign up for my newsletter to get notified for new articles!