When creating an immutable data structure, we often need to have a program that contains some state to mutate during the execution.

One example is creating an immutable queue. In the scala library, you initialized an immutable queue like this:

val empty = Queue[Int]()

Then, you can enqueue a queue, which returns a new queue with the updated element. You can also dequeue a queue, which returns a tuple of the element that you remove, and the new queue.

val one = empty.enqueue(1)
val (one, emptyQ) = one.dequeue()

However, if you want to do a series of operations with the immutable queue, you need to pass the new element to the next operation. Like this:

val one = empty.enqueue(1)
val two = one.enqueue(2) // enqueue from one
val three = two.enqueue(3) // enqueue from two

It causes a lot of error-prone if you need to do many operations by explicitly passing off one state to the other.

In this article, I want to share how you can use the cats State monad to construct queue. By using State monad, constructing an immutable data structure does not need to pass one state to another explicitly. Hence, it decreases the amount of error-prone boilerplate.

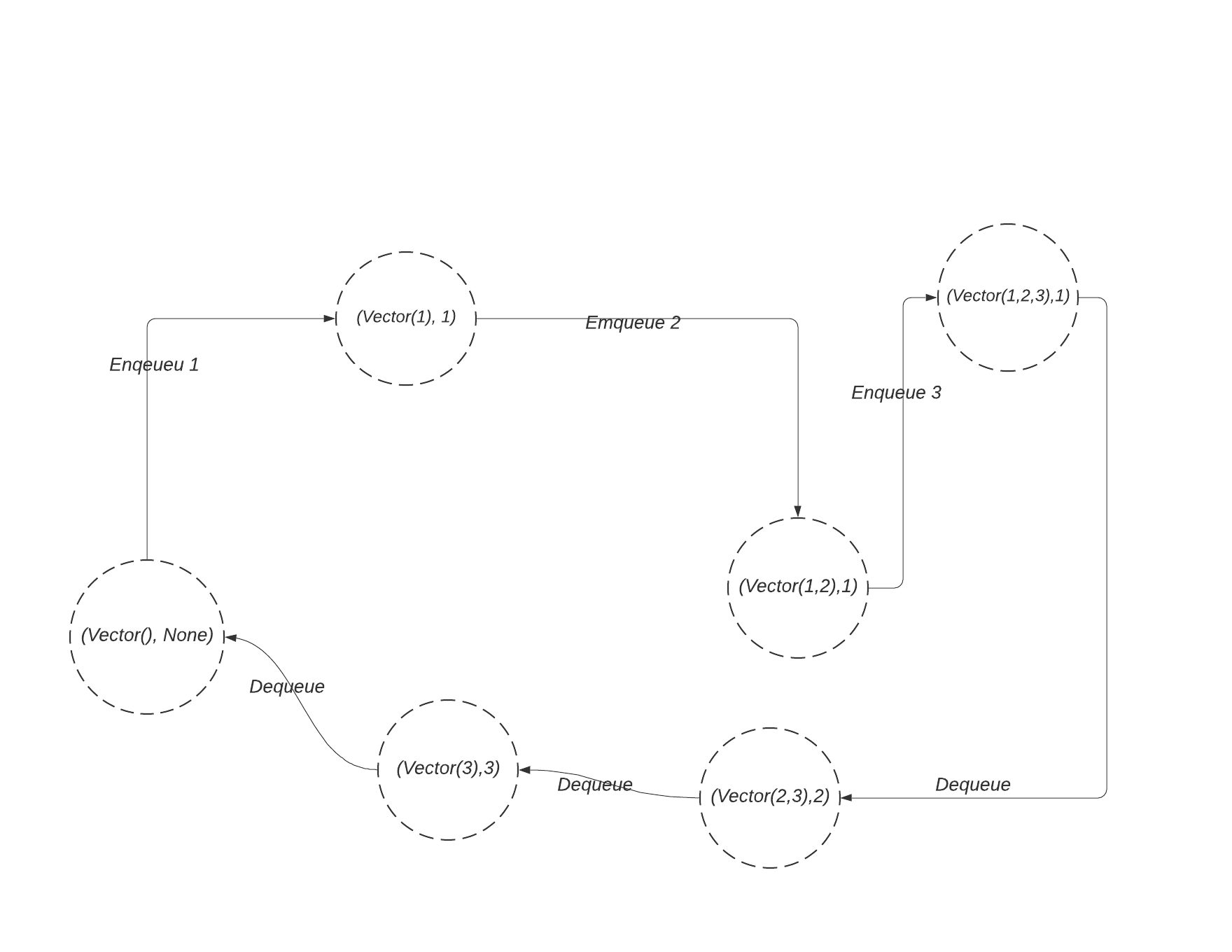
Order of execution

We start by implementing the regular immutable queue, which shows the same operation of a regular scala immutable queue. Then, we implement the same immutable queue, but with Cats State Monad.

Disclaimer: the queue implementation highly

Create Regular Immutable Queue

Let’s create the constructor of the queue:

class FunctionalQueue[+A](vector:Vector[A])

The main class of the FunctionalQueue contains a vector to contain all the elements that are enqueued or dequeue.

Let’s implement the enqueue and dequeue function:

def enqueue[B >: A](elmt:B): FunctionalQueue[B] = new FunctionalQueue(vector :+ elmt)
def dequeue: (A, FunctionalQueue[A]) = (vector.head, new FunctionalQueue[A](vector.tail))

The enqueue and dequeue function simply appending the value to the vector and retrieving the value from the vector.

Now, add a factory method for the FunctionalQueue constructor by defining the companion object.

object FunctionalQueue {
  def apply[A]():FunctionalQueue[A] = new FunctionalQueue[A](Vector.empty[A])
}

You can evoke the function in main, like this:

println(s"creating immutable queue without State monad")
val functionalQueue = FunctionalQueue[Int]
println(s"enqueue 1 immutable queue")
val enqueue1 = functionalQueue.enqueue(1)
println(s"enqueue 2 immutable queue")
val enqueue2 = enqueue1.enqueue(2)
println(s"front ${enqueue2.front}")
val (head, rest) = enqueue2.dequeue
println(s"dequeue head: ${head}  rest : ${rest}")

What is State Monad

According to Scala with Cats, the State monad allows us to pass additional state around as part of a computation.

The representation of the State instance is State[S,A], where it represents the function S => (S,A).

It means it takes in some state, and return a result along with the newly computed state.

Let’s try creating a simple state:

import cats.data.State
val a = State[Int,String] {integerState =>
  (integerState, s"The state is ${state}")
}

The state wires all the computations before the first input variable is ready to pass in. After the program is all wired, you can pass in the initial state, and execute run to get the expected end state and its result.

val (endState, result) = a.run(2).value // 2 is the initial input that is passed in
// endState: 2 result : The state is 2

The power of the state lies in the map and flatMap functionality. It can thread the state from one instance to another.

Each state represents an individual transformation, and you can combine them by using flatMap to transform the complete sequence of changes:

In the below example, plus1 and plus2 returns a value of the computed new State and the description history of that computation.

import cats.data.State

val plus1 = State[Int, String]{state =>
  (state+1, s"The result of this state is ${state+1}")
}

val plus2 = State[Int,String] {state =>
  (state +2, s"The result of this state is ${state+2}")
}

val program = for {
  historyOne <- plus1 // historyOne is the String
  historyTwo <- plus2
} yield List(historyOne, historyTwo)

val (result, history) = program.run(0).value
// result = 3
// history = List("The result of this state is 1","The result of this state is 3" )

As you can see, plus1 and plus2 is threaded even if we don’t interact with it in for comprehension.

Refactor Functional Queue with State Monad

Now that you know how State monad works let’s refactor the Functional Queue by using State monad.

Implement enqueue and dequeue with State monad.

type QueueFunc[A] = State[Vector[A], Option[A]]

def enqueue[A](elmt:A): QueueFunc[A] = State[Vector[A], Option[A]]{ oldVector =>
    (oldVector :+ elmt, oldVector.headOption)
  }

def dequeue[A]: QueueFunc[A] = State[Vector[A],Option[A]] { oldVector =>
  (oldVector.tail, oldVector.headOption)
}

I created QueueFunc as type alias that represent the State[Vector[A], Option[A]]. The State contains a Vector which contains a type A, and the optional head of the queue. The functions, enqueue and dequeue, take in an old vector and append or remove the head of the vector.

There you have it, we have done all of our implementation of the Immutable Queue with State!

How do you run the function?

Let’s execute the same operation as FunctionalQueue with our new implementation.

Remember, we use flatMap to combine each operation without really interacting with its updated state.

We supply all the expected steps of execution. Then, we wire it a program that supplies its initial state and execute the run function. In this case, the initial value is an empty Vector.

// supply our operation
val program = for {
  _ <- enqueue[Int](1)
  _ <- enqueue[Int](2)
  end <- dequeue[Int]
} yield end


val (newState, head) = program.run(Vector.empty[Int]).value
// newState = Vector(2)
// head = 1

Takeaway

• The State monad helps you eliminate all the error-prone boilerplate code that passes around the updated state to the next operation.
• The State monad instance passes in a State and returns the result along with its updated state.
• The power of State monad relies on map and flatMap operation, which threads one instance to another. Each state instances represent an atomic transformation. Their combination represents a sequence of changes. You don’t need to interact with the intermediary state in the for comprehension.

All information and example are in Github.

The GitHub information has 3 different approaches to implementing an immutable queue. The first one is the regular immutable queue without the state monad (first example). The second one mimics the regular immutable queue interface with State monad—the last implement stable state with State monad (2nd example of this article).

Like this Article?

Sign up for my newsletter to get notified for new articles!