Graph coloring is a problem that assigned certain kinds of color in the graph for a particular constraint. For instance, it can be a problem where given a graph, color the graph, either vertices or edges, so that no two colors are adjacent to each other. No two adjacent vertices or edges will have the same color.
I stumble upon understanding this algorithm, and I was thinking on my own the purpose of having this algorithm. As I look into Graph Coloring problems and their use cases, I realized that it is widely used in the applications we used. Therefore, this article will briefly talk about its algorithm, and use cases of Graph Coloring.
The Algorithm
There are many ways of graph coloring problems. You can do vertex coloring, edge coloring, Geographic Map coloring, and different questions you can ask in this algorithm. For instance, we can answer the questions of not assigning the same resources dependent on each other at the same time. We can also answer the questions of what is the minimum number of colors needed to color this graph. Moreover, we can make this into a backtracking questions, where we want to find all possible coloring method that can color this graph.
This will be a simple use-case. Once we know the basic algorithm, we can always answer these questions.
Let’s assume it is vertex coloring, where I want to color the graph so that no two adjacent vertexes have the same color.
Let’s assumed we have five vertices in a graph. The maximum amount of color that we can assign to each of the vertices can be 5. Therefore, we can initialize our list of colors to have five colors.
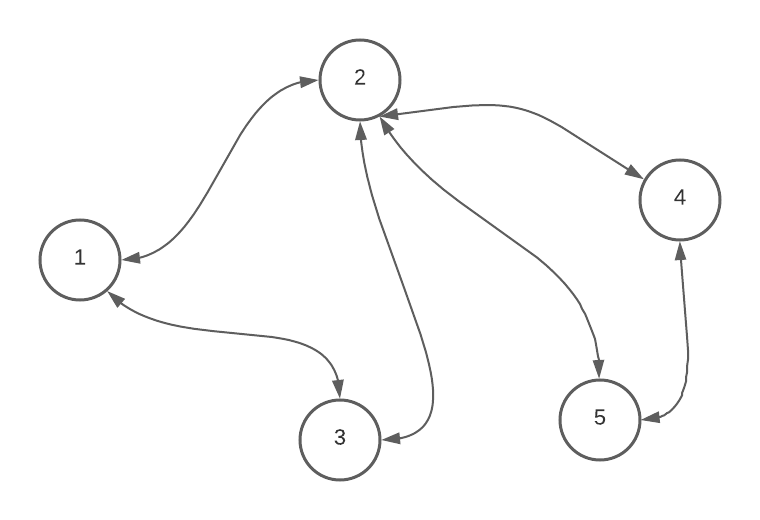
Next, we can start coloring the first vertex on a blank graph. You can choose any random one. It doesn’t matter.
In the following algorithm, we will color each vertex in the graph based on this operation:
- loop through all its neighbor vertices. If the adjacent vertex has color, but that color into a bucket (set).
- Choose the first color that is not in that bucket (collection), and assign it to the current vertex.
- Empty the bucket, and go to the next vertex that is not yet colored.
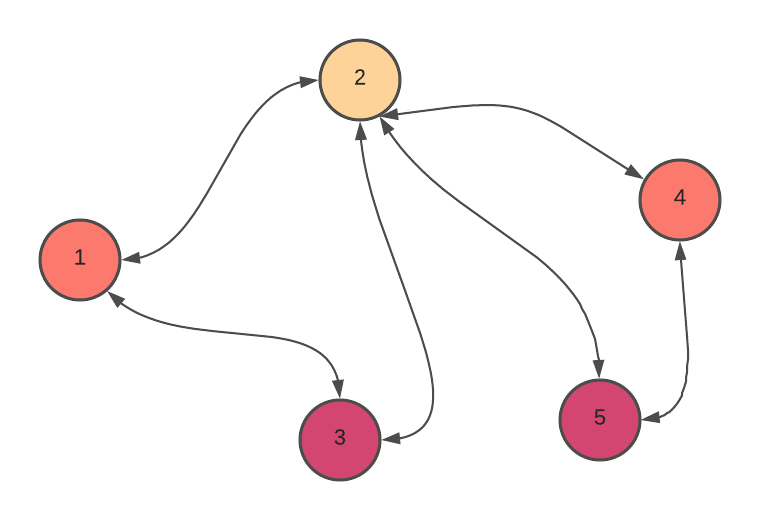
This greedy algorithm is sufficient to solve the graph coloring. Although it doesn’t guarantee the minimum color, it ensures the upper bound on the number of colors assigned to the graph.
We iterate through the vertex and always choose the first color that doesn’t exist in its adjacent vertice. The order in which we start our algorithm matters.
If the vertices that we iterate have fewer incoming edges, we might need more color to color the graph. Therefore, there is another algorithm called the Welsh-Powell Algorithm.
I want to explain how Welsh-Powell Algorithm works. To prove that it will be guaranteed a minimum number of coloring in a graph, you can check out the resources below. There are plenty of things to dive deep into this topic.
The algorithm is as follows:
- Count the incoming edges on each vertex, and sort them in descending order
- Choose the first vertex with the most incoming order and assign the vertices to a color. Let’s call it vertex A.
- Loop through the other vertices, assign the vertices a color if only if 1.) it is not the adjacent of the vertex A. 2.) The vertices have not yet been colored. 3.) That vertex’s neighbor doesn’t have the same color as vertex A.
- Keep doing step 3 until all the vertices are colored.
Now that you get a glimpse of what a graph coloring algorithm looks like, you might be wonder, what is the use of doing this?
Use Cases
Usually, the graph coloring algorithm is used to solve problems where you have a limited amount of resources and other restrictions. The color is just an abstraction of whatever resources you are trying to optimize, and the graph is an abstraction of your problem.
Graphs are often model as real-world problems, and we can use algorithms to find any attributes within the graph to answer some of our questions.
Here are some of the uses cases of Graph coloring:
Scheduling Algorithm
Imagine you have a set of jobs to do and several workers. It would help if you assigned the workers to a job during a specific time slot. You can assign jobs in any order, but a pair of jobs may be conflicted in a timeslot - because they share the same resources. How do you ensure that you assigned jobs efficiently so that no jobs are conflicted? In this case, vertices can be jobs, and the edges can be the connection of two jobs if they rely on the same resources. If you have an unlimited number of workers, you can use the Graph coloring algorithm to get the optimal time to schedule all jobs without conflict. In this case, the color will be the number of the worker. If the same color is assigned to the two vertices (jobs), that worker will handle those two jobs.
Another example is making a schedule or time table. You want to make an exam scheduler. Each subject will have a list of students, and each student will take multiple classes. You want to make sure that the exam that you schedule will not be a conflict for the students who take them. You don’t like to schedule an exam where the student who took that exam is conflicted with other classes’ exams. In this case, the vertices can be class, and there will be an edge between two classes if the same student is in both classes. The color in the graph, in this case, will be the amount of time slot needed to schedule the exams. So the same color on vertex A and vertex B means that A and B will be conducted at the same time slot.
Usually, there are shared resources in this type of problem, and we want to have a scheduler to schedule so that no two entities in your system are conflicted. The color usually represents the time slot or workers.
Map Coloring
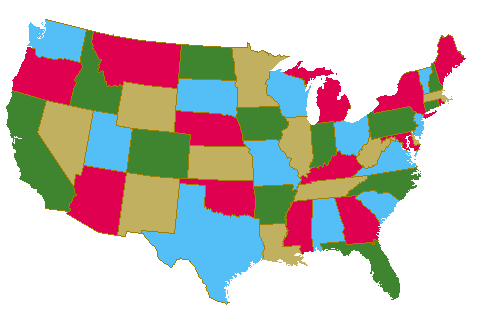
Geographical map coloring is a country or state where no two adjacent cities can be assigned to the same color. According to the four-color theorem, four colors are sufficient to color any map. In this case, the vertex represents each region, and each of its adjacents can be classified as an edge.
Sudoku Puzzle
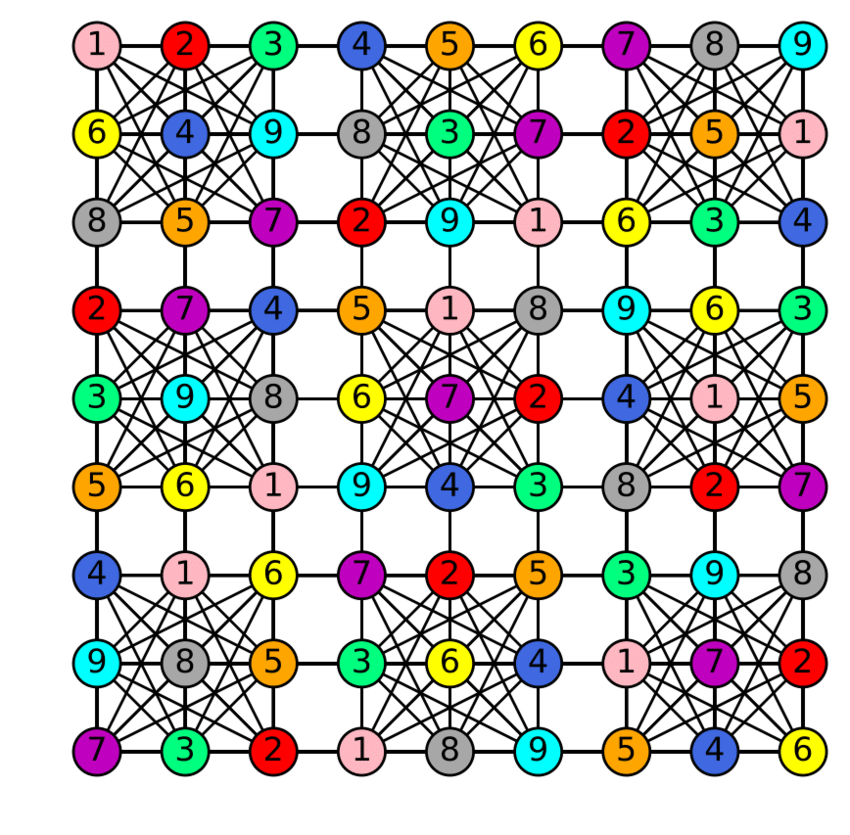
Sudoku is also a variation of the Graph Coloring problem where every cell represents a vertex. An edge is formed within two vertices if they are in the same row, column and block. Each block will have a different color.
Register Allocation for Compiler
A compiler is a program that transforms source code from high-level (Java, Scala) to machine level code. This is usually done in separate steps, and one of the very last steps is to allocate registers to the most frequent values of the programs while putting other ones in memory. We can model the symbolic registers (variables) as vertices, and an edge is formed if two variables are needed simultaneously. If the graph can be colored in K color, then the variables can be store in k registered.
There are tons of other use cases of graph coloring algorithms. I hope you learn something after reading through this far about Graph Coloring.
Resources
There are some great resources on the Graph Coloring algorithm, as well as its use cases. If you are curious to learn more, check out the resources below!
